Rivista di formazione e aggiornamento di pediatri e medici operanti sul territorio e in ospedale. Fondata nel 1982, in collaborazione con l'Associazione Culturale Pediatri.
Settembre 2006 - Volume IX - numero 7
M&B Pagine Elettroniche
Pillole di statistica
Specchio
specchio delle mie brame...dimmi quanti pazienti dovrò
arruolare?
UO
di Pediatria Ospedale San Giacomo Castelfranco Veneto (TV)
Indirizzo
per corrispondenza: dradzik@tiscali.it
Valutando
gli esiti di uno studio clinico dobbiamo sempre tenere
presente la possibilità che gli Autori siano giunti a dei
risultati errati principalmente per due ragioni:
- i ricercatori possono aver concluso che due trattamenti sono differenti tra di loro quando, in effetti, non lo sono, compiendo unerrore di tipo I o alfa (questo tipo di errore misura la probabilità di arrivare a delle conclusioni falsamente positive). Convenzionalmente si cerca di ridurre la probabilità che esso si verifichi al di sotto del 5% (p <0.05);
- i ricercatori possono aver concluso che due trattamenti non sono differenti quando, in effetti lo sono, compiendo un errore di tipo II o beta (questo tipo di errore misura la probabilità di giungere a delle conclusioni falsamente negative); anche in questo caso è stato posto arbitrariamente il limite del 20% di probabilità con la quale si desidera evitare di compiere un tale errore (β <0.20).
Matematicamente
il potere di uno studio è il complemento dell'errore di tipo
β (1- β) e rappresenta la probabilità di evitare una
conclusione falsamente negativa. In altre parole è la
probabilità pre-studio che la ricerca sia in grado di
identificare (per un dato livello di significatività, per es.
p<0.05) una differenza minima considerata dagli Autori come
clinicamente significativa.
Il potere
deve essere calcolato prima dell'inizio dello studio e serve per
stabilire la numerosità campionaria.
Ma dato
queste premesse, come possiamo accorgerci se uno studio ha arruolato
un numero sufficientemente ampio di pazienti?
Per prima
cosa osserviamo gli Intervalli di Confidenza (IC) presenti
nell'articolo.
Intervalli
di Confidenza, significatività statistica e clinica
Bisogna
considerare che i ricercatori non sono in grado di coinvolgere nel
loro trial tutta la popolazione disponibile, ma solo un suo campione
rappresentativo: i risultati trovati non esprimono con sicurezza
dunque il vero valore della popolazione, ma solo una sua stima, per
giunta imprecisa. Il grado di incertezza è ben rappresentato
dagli Intervalli di Confidenza (IC), che dovrebbero sempre essere
associati ai dati e che costituiscono il range dei possibili veri
valori dell'intera popolazione nel 95% dei casi; più ampi
essi sono, più i risultati saranno imprecisi e maggiore sarà
la confidenza che lo studio sia in realtà troppo “piccolo”
per individuare delle differenze; più grande è invece
lo studio, più piccolo sarà probabilmente l'errore
compiuto e più preciso il risultato: ecco che studi di grande
numerosità possono perciò raggiungere facilmente una
significatività statistica.
Per
giudicare se un intervento sia veramente utile, non ci si deve
limitare a osservare la sola significatività statistica, ma è
necessario verificare anche che il range (IC 95%) delle possibili
differenze riscontrato fra i due gruppi (di solito attivo e placebo)
includa soltanto effetti clinicamente importanti. La Figura
1 dimostra come la posizione degli IC 95% (relativamente alla
linea dell'ipotesi nulla di nessuna differenza fra i due
trattamenti e alla linea dell'importanza clinica) chiarisca bene
l'effetto della terapia in termini di significatività
statistica e clinica: idealmente un trattamento per essere
raccomandato deve essere sia statisticamente che clinicamente
significativo (gli Intervalli di Confidenza al 95% devono includere
cioè valori situati sempre al di sopra della linea di
importanza clinica).
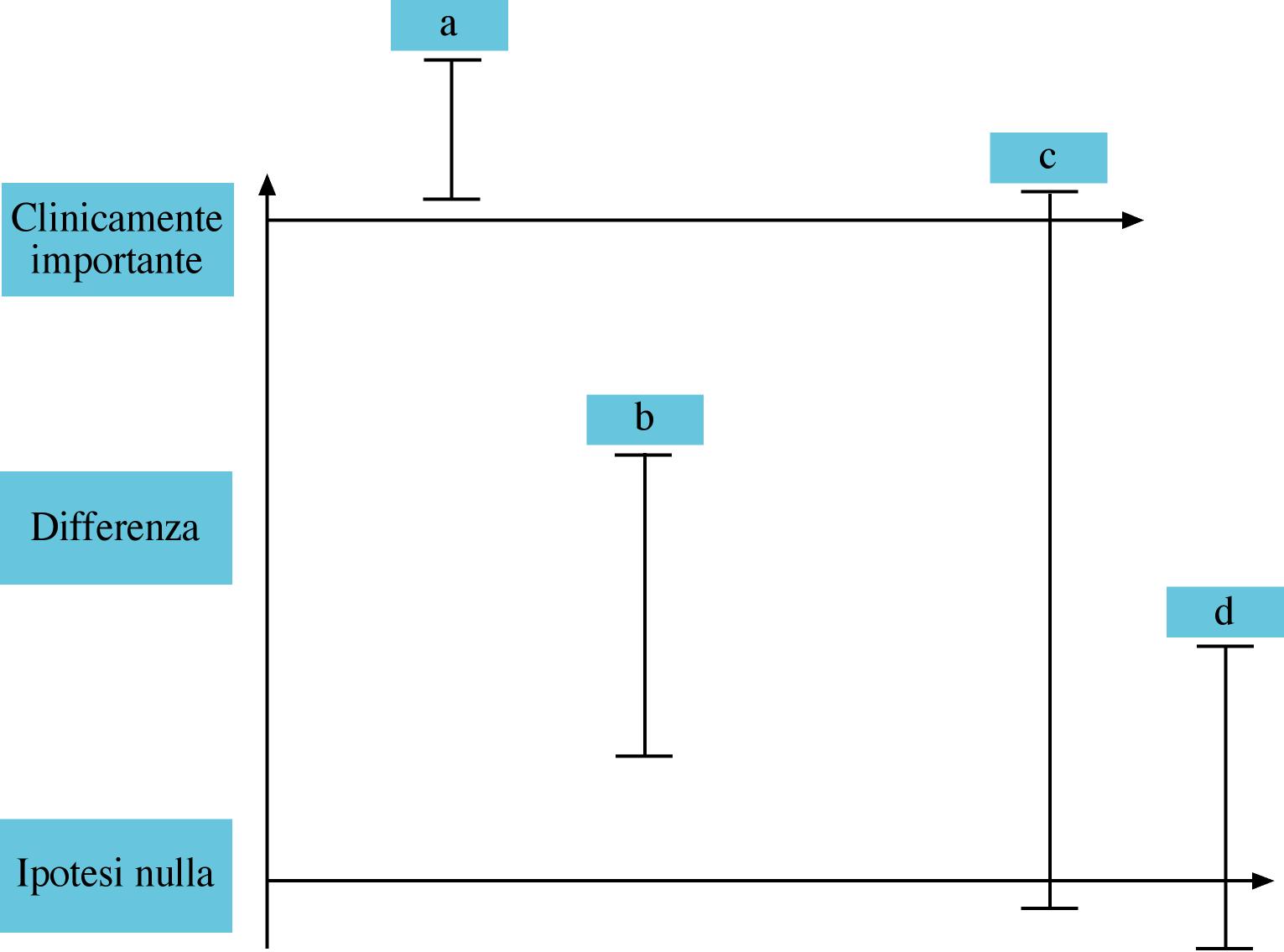
Figura
1. Distinzione fra significatività statistica e importanza
clinica
Legenda:
le barre verticali rappresentano gli Intervalli di Confidenza
al 95% intorno alle differenze fra il trattamento e il controllo.
Sull'asse
delle ordinate sono registrati i valori delle differenze fra i due
gruppi.
La linea
dell'ipotesi nulla rappresenta l'ipotesi di partenza, cioè
che il trattamento attivo e il placebo determinino effetti uguali.
La linea
dell'importanza clinica rappresenta il limite per
considerare utile (clinicamente efficace) un intervento.
a.
Differenza statisticamente significativa e clinicamente importante.
b.
Differenza statisticamente significativa, ma clinicamente non
importante.
c.
Differenza è statisticamente non significativa e di incerta
importanza clinica.
d.Differenza non statisticamente significativa e clinicamente non
importante.
Il
potere dello studio e il calcolo della numerosità campionaria
Facciamo
ora un esempio: in un articolo gli Autori, nel capitolo metodi,
riportano che il loro studio aveva il 90% di probabilità
(potere) di riuscire a identificare tra trattamento attivo e
placebo una differenza del 40%, che era stata considerata essere
clinicamente significativa.
Gli
investigatori avevano ricavato da precedenti studi come la frequenza
dell'evento nel gruppo di controllo (non in trattamento) risultasse
intorno al 10% (p2 =0.10). Su questa base avevano
calcolato a priori, prima di iniziare il loro studio, che se avessero
riscontrato una riduzione della frequenza dell'evento nel gruppo
attivo del 40% o, detto in altri termini, una frequenza nel gruppo in
trattamento del 6% (0.06) (p1= 0.10-0.04=0.06), questo
sarebbe stato un risultato utile.
Definito
R il rapporto fra i due rischi p1/p2 (=6%/10%
=0.6) e assumendo di voler avere il 90% di probabilità di
identificare tale differenza [(tenendo in considerazione comunque che
in ogni caso c'erano < 5% (p<0.05) di possibilità che
il risultato fosse falsamente positivo] determiniamo la numerosità
campionaria applicando la seguente formula (1). La variabile 10.51
rappresenta una costante per i valori di alfa =0.05 e beta =0.90.
n =
10.51[(R+1) - p2(R2+1)]/ p2(1-R)2
n =
10.51[(0.60+1)-0.10(0.602+1)]/0.10(1-0.60)2 =
961,665 ≈ 962 pazienti per ciascun gruppo.
Se
fissiamo dei valori diversi per l'errore alfa e per il potere dovremo
modificare l'ampiezza del campione e la costante (Tabella
1): ridurre alfa o aumentare il potere determinano in ambedue i
casi un innalzamento del campione richiesto: per esempio una
riduzione di alfa da 0.05 a 0.01 (cioè voler diminuire la
probabilità dal 5% all'1% di essere giunti a delle
conclusioni falsamente positive) comporta un aumento del 70% della
numerosità campionaria richiesta al potere = 0.50, del 50% al
potere di 0.80; con alfa = 0.05 un incremento del potere da 0.50 a
0.80 richiede il doppio del campione e da 0.50 a 0.99 il quintuplo
(Tabella 2).
Potere
(1-β) | |||
0.80 | 0.90 | 0.95 | |
Alfa
(errore di tipo I) | |||
0.05 | 7.85 | 10.51 | 13.00 |
0.01 | 11.68 | 14.88 | 17.82 |
Sostituire
il valore di 10.51 con il valore appropriato ricavato.
Si
considerano di solito sufficienti i seguenti limiti: alfa = 0.05 e
potere = 0.80.
Tabella
2. Numerosità campionaria approssimativa richiesta per
differenti livelli di alfa e di potere
Potere
(1-β) | ||||
0.50 | 0.80 | 0.90 | 0.99 | |
Alfa
(errore di tipo I) | ||||
0.05 | 100 | 200 | 270 | 480 |
0.01 | 170 | 300 | 390 | 630 |
0.001 | 280 | 440 | 540 | 820 |
Per
complicare le cose
Dobbiamo
tener presenti alcuni fattori che possono influenzare il calcolo
della numerosità campionaria:
- La frequenza degli eventi nel gruppo di controllo viene di regola fornita agli investigatori dai risultati di precedenti studi pubblicati, ma non sempre questi dati sono disponibili; inoltre è necessario tener conto pure degli scenari, criteri di eleggibilità e trattamenti diversi presenti;
- il giudizio su cosa si intenda per effetto “clinicamente significativo” è soggettivo, perché per alcuni ricercatori, una riduzione del 10% nella frequenza degli eventi è clinicamente utile, per altri è necessario un limite superiore, diciamo del 20% o del 30%. Tenendo costante la frequenza dell'evento nel gruppo di controllo, per ridurre della metà l'ampiezza dell'evento è richiesto un aumento di 4 X della numerosità campionaria: nell'esempio precedente partendo da una frequenza dell'evento nel gruppo di controllo del 10% e da quella considerata efficacemente utile nel gruppo attivo del 6% (riduzione del 40%), abbiamo calcolato come la numerosità del campione richiesta fosse di circa 965 pazienti per ciascun gruppo. Se ci accontentassimo invece di una frequenza dell'evento inferiore nel gruppo di trattamento, diciamo dell'8% (cioè di una riduzione del 20%), sarebbe richiesto un numero di pazienti 4 volte superiore (4298).
n =
10.51[(R+1) – p2(R2+1)]/ p2(1-R)2
n =
10.51[(0.80+1)-0.10(0.802+1)]/0.10(1-0.80)2 =
4298 per ciascun gruppo.
Molto
spesso gli investigatori, specie nel caso di eventi a frequenza rara
si trovano a realizzare uno studio che ha un basso potere, arruolando
un numero di pazienti molto più ridotto di quello considerato
necessario. Anche questo genere di trial comunque ha una sua dignità,
perché i suoi risultati possono essere combinati assieme a
quelli di altri studi simili in una meta-analisi, dando in questo
modo informazioni assai utili (2).
Bibliografia
- Shulz KF, Grimes DA. Sample size calculations in randomised trias: mandatory and mystical. Lancet 2005;365:1348-53.
- Chalmers TC, Levin H, Scks HS, Reitman D, Berrier J, Nagalingam R. Meta-analysis of clinical trials as a scientific discipline, I: control of bias and comparison with large co-operative trials. Stat Med 1987;6:315-28.
Vuoi citare questo contributo?
